Loi de probabilité usuelles

Lois de probabilité discrètes

Loi de Bernoulli

Considérons un processus aléatoire avec une variable aléatoire \(X\) avec deux résultats possibles: succès ou échec. Cela correspond au tirage d’une pièce avec comme résultat pile ou face. Pour chaque résultat on associe une valeur 0 ou 1: pour un succès, \(X=1\) et pour un échec, \(X=0\). La probabilité d’obtenir un succès vaut \(p\), celle d’obtenir un échec vaut donc \(1-p\). La loi de probabilité, aussi appelé loi de Bernoulli de paramètre \(p\), peut alors s’écrire:

(31)\[\begin{equation} P(x;p) = p^x(1-p)^{1-x}. \end{equation}\]

Loi binomiale

Si on répète \(n\) fois une expérience de Bernoulli de façon indépendante et on compte le nombre de succès parmi ces \(n\) tentatives, la probabilité d’obtenir \(k\) succès (et donc \(n-k\) échecs) est donnée par la loi binomiale. L’ordre des succès et échecs n’important pas, le nombre de combinaisons de \(k\) succès parmi \(n\) tentatives correspond au coefficient binomial \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\) et la probabilité pour chaque combinaison vaut \(p^k (1-p)^{n-k}\). La probabilité binomiale vaut donc:

(32)\[\begin{equation} P(k; n,p) = \binom{n}{k}p^k (1-p)^{n-k}. \end{equation}\]

Le nombre moyen de succès \(\bar{k}\) parmi \(n\) lancers est donné par:

(33)\[\begin{equation} \bar{k} = \mathbb{E}(k) = \sum _{k=0}^N k\times P(k; n,p) = n\times p \end{equation}\]

et la variance du nombre de succès vaut:

(34)\[\begin{equation} \sigma_k^2 = \sum _{k=0}^N (k-\bar{k})^2\times P(k; n,p) = np(1-p). \end{equation}\]

Lorsqu’on souhaite extraire la probabilité \(p\) de succès à partir de \(k\) succès parmi \(n\) essais, on peut utiliser la relation:

(35)\[\begin{equation} \bar{p} = \frac{k}{n}. \end{equation}\]

On voit donc que \(\mathbb{E}(\bar{p}) = \mathbb{E}(k/n) = p\) et que

(36)\[\begin{equation} \sigma_{p} = \frac{\sigma_k}{n} = \sqrt{\frac{p(1-p)}{n}}. \end{equation}\]

Loi de Poisson

La loi de Poisson s’applique aux processus de comptage pour lesquels on compte le nombre de succès pendant une durée de temps fixée. Si on divise la durée de temps \(\Delta t\) en \(N\) morceaux et on note \(p\) la probabilité d’avoir un succès pendant cette période, le nombre moyen de succès est alors \(Np\) et est donc proportionnel à \(\Delta t\). Cette approche est valide lorsque la probabilité de succès \(p\) est faible (mais avec \(\lambda = Np\) non nul): dans ce cas, la probabilité d’observer \(k\) succès pendant \(N\) morceaux suit une loi binomiale:

(37)\[\begin{equation} P(k; n,p) = \binom{n}{k}p^k (1-p)^{n-k} = \frac{n!\lambda ^k}{k!(n-k)!n^k}\left( 1-\frac{\lambda}{n} \right) ^{n-k}. \end{equation}\]

Or si \(p\) est très petit devant 1, \(N\) est très grand devant 1 et alors

(38)\[\begin{equation} \frac{n!}{(n-k)!n^k} \approx \frac{n^k}{n^k} = 1 \end{equation}\]

(39)\[\begin{equation} \left( 1-\frac{\lambda}{n} \right) ^{n-k} \approx \left( 1-\frac{\lambda}{n} \right) ^{n} \approx \left(\exp -\frac{\lambda}{n}\right)^n = e^{-\lambda}. \end{equation}\]

On a donc la définition de la loi de probabilité de Poisson:

(40)\[\begin{equation} P(k; \lambda) = \lim _{n\rightarrow \infty; p\rightarrow 0} P(k; n,p) = \frac{e^{-\lambda}\lambda ^k}{k!}. \end{equation}\]

La figure ci-dessous montre des distributions de Poisson avec plusieurs valeurs du paramètre \(\lambda\).

import matplotlib.pyplot as plt # importer maplotlib
import numpy as np
from scipy.stats import poisson
from math import exp, sin, pi, cos

# poissonList = np.random.poisson(5,1000000)
xx = [val for val in range(0,20)]

fig, ax = plt.subplots() # creation d'un plot
line, = ax.plot(xx,poisson.pmf(xx, 3.),"-",marker="o",label="Poisson(k,3)") # plot de y1 vs x
line, = ax.plot(xx,poisson.pmf(xx, 5.),"-",marker="o",label="Poisson(k,5)") # plot de y1 vs x
line, = ax.plot(xx,poisson.pmf(xx, 10.),"-",marker="o",label="Poisson(k,10)") # plot de y1 vs x
# n, bins, patches = plt.hist(poissonList, bins=np.arange(-0.5, 15.5, 1.), alpha=0.75, label="Gen. poisson", density=True)
ax.set_ylim(bottom=0.)
ax.set_ylabel('k') # titre de l'axe x
leg = ax.legend()   # creation de la légende

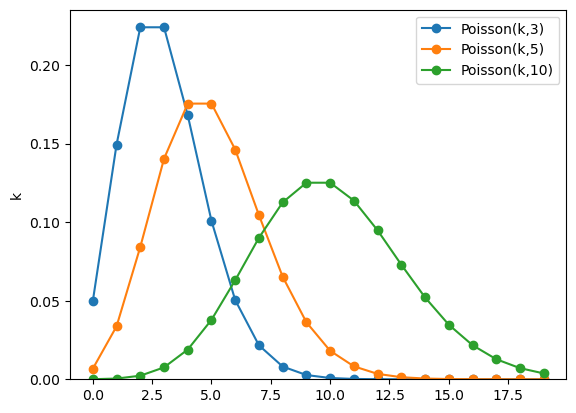
On remarque que la distribution n’est pas symétrique autour de la valeur de \(\lambda\), pour les valeurs de \(\lambda\) faibles; cependant à partir de \(\lambda=10\), on peut voir que la distribution devient relativement symétrique et de forme gaussienne (voir section Loi normale ou loi de Gauss).

Les caractéristiques de la loi de Poisson découle de celles de la loi binomiale. En utilisant le fait que \(\lambda = np\) et que \(p \ll 1\), le nombre moyen de succès \(\bar{k}\) est donné par:

(41)\[\begin{equation} \bar{k} = \mathbb{E}(k) = \sum _{k=0}^{\infty} k\times P(k; \lambda) = \lambda \end{equation}\]

et la variance du nombre de succès vaut:

(42)\[\begin{equation} \sigma_k^2 = \sum _{k=0}^\infty (k-\bar{k})^2\times P(k; \lambda) = \lambda. \end{equation}\]

L’écart-type d’une distribution de Poisson vaut donc \(\sqrt{\sigma _k ^2} = \sqrt{\lambda}\).

Exercise 6

Certaines espèces de tortues pondent de nombreux oeufs (110 pour certaines). La distribution du nombre d’oeufs pondus suit une loi de Poisson de paramètre \(\lambda=110\).

1. Rappeler la loi de Poisson; que vaut la moyenne du nombre d’oeufs?

2. Tous les oeufs n’arriveront pas à maturité; on peut considérer que la probabilité qu’un oeuf arrive à maturité est indépendante du nombre d’oeufs pondus et vaut \(p\). Si le nombre d’oeufs est \(n\), quelle est la loi de probabilité associée à l’éclosion de \(k\) oeufs parmi les \(n\) oeufs?

3. Démontrer que la loi de probabilité du nombre d’oeufs pondus et arrivant à l’éclosion est une loi de Poisson de paramètre \(\lambda \times p\).

Solution to Exercise 6

1. La loi de Poisson décrit la probabilité d’obtenir \(k\) sachant que le nombre moyen est \(\lambda\):

   (43)\[\begin{equation} \mathcal{P}(k;\lambda) = \frac{e^{-\lambda}\lambda ^k}{k!}. \end{equation}\]

   Ici, le nombre moyen d’oeufs est donc \(\lambda\).

2. C’est une loi binomiale:

   (44)\[\begin{equation} \mathcal{B}(k;n) = \left(\begin{matrix} n\\ k \end{matrix}\right) p^k (1-p)^{n-k}. \end{equation}\]

3. La probabilité d’obtenir \(k\) oeufs éclos pour une ponte est donc la probabilité de pondre \(r\) oeufs et que parmi ces \(r\), \(k\) éclosent. On remarque qu’il faut au moins \(r=k\) oeufs pondus pour avoir \(k\) oeufs éclos.

   \[ P_{\mathrm{oeufs}}(k; \lambda, p) = \sum_{r=k} ^\infty \mathcal{P}(r;\lambda)\times \mathcal{B}(k;n) \]
   \[\begin{split} = \sum _{r=k}^\infty \frac{e^{-\lambda}\lambda ^r}{r!}\left(\begin{matrix}r\\k\end{matrix}\right) p^k (1-p)^{r-k}p^k(1-p)^{r-k} \end{split}\]
   \[ = e^{-\lambda}p^k(1-p)^{-k} \sum _{r=k}^\infty \frac{\lambda ^r}{r!}\frac{r!}{k!(r-k)!}(1-p)^r \]
   \[ = e^{-\lambda}p^k(1-p)^{-k} \frac{\lambda ^k(1-p)^k}{k!} \sum _{r'=0}^\infty \lambda ^{r'}(1-p)^{r'} \]
   \[ = e^{-\lambda}p^k(1-p)^{-k} \frac{\lambda ^k(1-p)^k}{k!} e^{\lambda(1-p)} \]
   \[ = \frac{e^{-\lambda p}(\lambda p)^k}{k!} = \mathcal{P}(k;\lambda p) \]

Lois de probabilité continues

Loi uniforme

La loi uniforme consiste à ce que toutes les intervalles de taille \(\mathrm{d}x\) sont équiprobables sur une gamme donnée. Plus précisément, la loi uniforme \(f(x)\) sur l’intervalle \(\left[ a,b \right]\) est définie par deux paramètres \(a\) et \(b\):

(45)\[\begin{equation} f(x;a,b) = \frac{1}{b-a} \end{equation}\]

pour \(a<x<b\) et nulle ailleurs.

Sa moyenne vaut \(\mu = \mathbb{E}[X] = \frac{a+b}{2}\) et sa variance \(\sigma ^2 = \frac{(b-a)^2}{12}\).

Loi normale ou loi de Gauss

Cette loi est l’une des plus utilisées en statistique, car elle définit de nombreux processus aléatoires et est le résultat de plusieurs théorèmes majeurs comme le théorème centrale limite. Cette loi est définie par deux paramètres \(\mu\) et \(\sigma\):

(46)\[\begin{equation} f(x; \mu, \sigma) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}. \end{equation}\]

La moyenne de cette distribution est \(\mu\) et sa variance est \(\sigma ^2\). Notons que la médiane et le mode de cette distribution sont égaux à la moyenne.

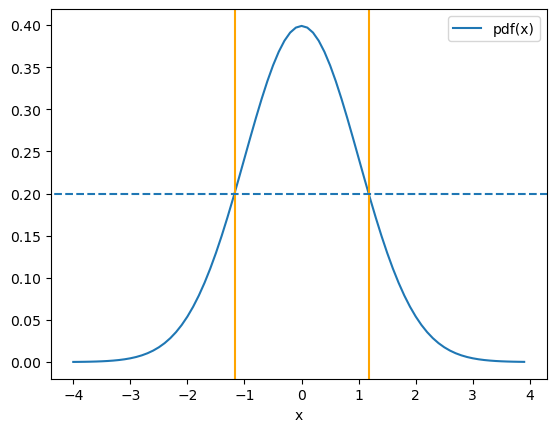
En sciences expérimentales, il est souvent plus simple de déterminer l’écart-type en utilisant la largeur à mi-hauteur (FWHM ou Full Width Half Maximum): elle est déterminée par la relation:

(47)\[\begin{equation} f(\mu+\mathrm{FWHM}/2; \mu, \sigma) = \frac{1}{2} f(\mu; \mu, \sigma) \Rightarrow \mathrm{FWHM} = 2\sqrt{2\ln 2}\sigma \approx 2.35 \sigma. \end{equation}\]

La forme de la distribution gaussienne ainsi que la largeur à mi-hauteur sont représentées sur la figure ci-dessous.

import matplotlib.pyplot as plt # importer maplotlib
import numpy as np
from scipy.special import erf

def gaussian(x, mu, sig):
    return 1./(np.sqrt(2*3.1415)*sig)*np.exp(-np.power(x - mu, 2.) / (2 * np.power(sig, 2.)))

x = [ 0.1*i for i in range(-40,40) ] # liste d'abscisses de la figure
y1 = [gaussian(val,0,1) for val in x]                          # calcul de y = f(x)

fig, ax = plt.subplots() # creation d'un plot
ax.plot(x,y1,"-",label="pdf(x)") # plot de y1 vs x
ax.set_xlabel('x') # titre de l'axe x
plt.axvline(-2.35/2., 0, 10, c='orange')
plt.axvline(2.35/2., 0, 10, c='orange')
plt.axhline(0.5/(np.sqrt(2*3.14159)), -2.35/2., 2.35/2., ls="--")
leg = ax.legend()   # creation de la légende